Talk:Flux
| This It is of interest to the following WikiProjects: | |||||||||||
‹See TfM›
| |||||||||||
|
Starting a rewrite (July 8 2016)
[edit]I started a full rewrite of the article. I cannot say I am really satisfied with the current result, and I would like to apologize for that - I thought I could get it done without using the sandbox, but I saw too big. Do share any opposition to the general philosophy of how the contents are dealt with though, even if the article will badly need a copyedit (but the former version was worse in that respect). TigraanClick here to contact me 16:49, 8 July 2016 (UTC)
- the previous page was fine. further, your english isn't sufficient to start making huge edits like this. wikipedia is not an editing service. i understand you want to contribute, but i am very suspicious about what motivated this "edit".
- @David Eppstein, Michael Hardy, D.Lazard, and Favonian: what do you think of this new "revision"? i find the figure far inferior and less informative than the old one (among other things). also, i find it suspicious because someone from india (User:G41rn8) randomly set the "expert needed" tag, to which someone else from india (User:Tigraan) miraculously answered, deleted a bunch of things and expected us to edit his work.
- one glaring, and obvious example of the poor quality of this "revised" page is when you compare the old figure:
F is a flux of the first sort, ∫F·dS is a flux of the second sort (through surface S). dS is the differential vector area element, n is the unit normal to the surface. Left: flux (type 2) is proportional to the component of flux (type 1) that flows normal to the surface. Right: The reduction in flux (type 2) through a surface can be visualized by reduction in F or dS equivalently (resolved into components, θ is angle to normal n). F·dS is the component of flux (type 1) passing though the surface, multiplied by the area of the surface (see dot product). For this reason the units of a type type 2 flux are unit area multiplied by its type 1 equivalent.
to the new one:
- this should have been taken to sandbox and i am going to revert. 174.3.155.181 (talk) 22:40, 10 July 2016 (UTC)
- Do revert if you want, I agree I should have gone through the sandbox and the end result was meh. However, the former article was far from "fine", and the figure change is a clear net positive in my view (not so much the figure itself, but the incomprehensible caption). Keep in my that "flux" is likely to attract readers who do not even know what a cosine is (unlike, say, Bessel's correction where we can assume readers to have some technical background).
- As for the WP:SOCK accusation, maybe a quick look at either my user page ("from India", really?) or my contributions would tell you something. I would appreciate if you retracted that, or alternatively took me to WP:SPI if you stand by your implied accusation. TigraanClick here to contact me 18:51, 11 July 2016 (UTC)
- Leave it as it is right now. I have reviewed both versions and although many of User:Tigraan's edits are good, many are also poor. I would suggest leaving it as it is now, and then (as we normally do in wikipedia) make small edits that other editors can comment on or improve before moving on to another section. This works best for everyone. I think User:Tigraan has already commented that he/she should have done it this way or sandboxed a big project like this, so lesson learned. StarHOG (talk) 15:19, 20 July 2016 (UTC)
Apologies for the bad diagram (it was mine). I like the newer one by user:Debenben also, feel free to replace. In the mean time I have fixed my old one with a new caption. M∧Ŝc2ħεИτlk 20:02, 20 July 2016 (UTC)
- I agree, that File:General flux diagram.svg is more informative. I created the new one for the German article because it fits better with the notation used in the text, i.e.
- in the German article, the surface element is called , (this article uses , the figure shows a scalar quantity )
- quantities that are not refered to in the text (at the moment ) are not shown in order to keep it simple and avoid confusion.
- In case you want to change File:General flux diagram.svg again, keep in mind it is used in other wikis, too.--Debenben (talk) 20:53, 20 July 2016 (UTC)
- Sorry for late reply. I must have misunderstood completely what the preference in diagrams was, people favored the old one after all. Thanks also for the clarification and heads up Debenben. M∧Ŝc2ħεИτlk 07:15, 23 July 2016 (UTC)
Misleading Sentence Under "Transport Fluxes"
[edit]> Also acts as a generalization of heat flux, which is equal to the radiative flux when restricted to the infrared spectrum.
Should read "Also acts as a generalization of heat flux, which is equal to the radiative flux when restricted to electromagnetic radiation" or similar. You should not imply that only infrared transports heat. 174.124.85.209 (talk) 11:39, 7 October 2017 (UTC)
 Done, but I believe the page is not protected, so you're welcome to edit the page yourself. Gap9551 (talk) 14:08, 7 October 2017 (UTC)
Done, but I believe the page is not protected, so you're welcome to edit the page yourself. Gap9551 (talk) 14:08, 7 October 2017 (UTC)
The terminology section is nearly impossible to follow
[edit]It refers to the "first definition" and appears to give two definitions in that sentence. Is the second half of the sentence a different definition? It says "vector field / function of position"; what does it mean to divide a vector field by a function of position?
Are these the two definitions?
First definition: flux is a single vector Second definition: flux is a vector field
The third sentence seems to contradict the second sentence.
The descriptions in the last paragraph are ambiguous. I think the only way someone would understand what is being said is if they already understood the definitions of the various terms.
A step in the right direction would be to clearly identify the two definitions. In the last paragraph, it would make sense to omit the word "flux" when referring to the definitions. Can someone who understands this clean it up?
128.174.126.83 (talk) 18:11, 6 February 2018 (UTC)
- I only changed the names "first definition" and "second definition" for "transport definition" and "electromagnetism definition", respectively, while respecting the original claim regarding the literature. I did check a bit the literature and it seems that the claim is correct that flux is some times used as a quantity that can be integrated over a surface and other times as the result of this integration. Dominic Mayers (talk) 20:37, 27 February 2019 (UTC)
Section: Flux as a Surface Integral
[edit]The "Flux as a surface integral" section and the accompanying image are confusing. Third row of image says "flux is proportional to area within boundary", in which flux is apparently meant as the surface integral and corresponds to rate/vector field in the transport definition. In the body text this image is referred to by: "See also the image at right: the number of red arrows passing through a unit area is the flux density", which I would assume be flux in transport terminology. Two paragraphs above this we have "Conversely, one can consider the flux the more fundamental quantity and call the vector field the flux density." in which the vector field would again be the conserved quantity. It would really be helpful to distinguish between the vector field, flux and flux density first.
Totally aside, I believe the concept of flux was introduced by Fourier long before Maxwell. Will look up references and add them if I can.
--144.122.162.45 (talk) 08:58, 23 June 2018 (UTC)
It seems that the section terminology addresses your point. It seems on purpose that we do not have a consistent definition of flux (and of flux density) throughout the article. Dominic Mayers (talk) 20:46, 27 February 2019 (UTC)
In laymen's terms: Flux density is the amount of flux per unit area. Similar to current density. Total flux describes the total amount of whatever the metric is referring to; heat, magnetic, photon, ect, but when it's described in terms of a per unit area (typically about the plane that runs perpendicular to the vector field, or whatever plane you are attempting to describe flux about, the plane doesn't always have to be perpendicular to the vector field), then it becomes flux density. — Preceding unsigned comment added by 64.179.179.8 (talk) 12:34, 28 February 2021 (UTC)
- Maybe this is a physics vs. engineering distinction. Engineers define flux as a rate of transfer (e.g., heat, mass) per unit area, i.e., what is called flux density in your and other comments. See for example p 13 in Bird et al. 2007 or p 4 in Bergman et al. 2011 for example. Sashahafner (talk) 11:51, 15 February 2023 (UTC)
- No, it depends on the field of study. In transport phenomena flux is a rate of transfer per unit time through a surface, such as fluid flow, heat, electric charge, momentum or mass transport. But in a field theory the flux of a field through a surface is not a rate, it has nothing to do with time, such as flux of a magnetic field, electric field, vector potential, etc. The only generalization you can make is that a flux is a surface integral of a flux density. --ChetvornoTALK 17:26, 15 February 2023 (UTC)
Flux vs. flux density
[edit]Speaking as a physicist in general, and a transport theorist in particular, I agree with the header that says this article is mixing up flux and flux density. As such I think this article is likely to confuse a lot of novice readers (e.g. physics students). The unfortunate thing is that many authors use the two terms interchangeably, and so it isn't so surprising that this article mixes them up. I don't have the time at the moment to try doing a rewrite of this article, but maybe I'll come back to this in a month or so after all my final exams are marked and have a go at it. The distinction made by the previous poster (28 Feb.) is what I think most experts would agree with.
A further criticism is that the statements in the introductory paragraph about whether flux is a vector or scalar an not correct. It is difficult to make a general statement about this because fluxes and flux densities of different types of quantities can be all sorts of different types of mathematical objects depending on the quantity being "transported". For example, in transport theory, momentum flux density is a 2nd rank tensor, and so momentum flux is a vector, but energy flux density is a vector and so energy is a scalar. In general (is this *fully* general? Ask a mathematician not a physicist like me...) if we have any flux density, q, then the associated flux will be whatever sort of quantity results from taking an inner product between q and a vector. — Preceding unsigned comment added by Gleedadswell (talk • contribs) 15:07, 20 March 2021 (UTC)
- @Gleedadswell: It would be great if you could find the time to do your proposed rewrite to clear up the confusion between flux and flux density and also to deal with the case where the flux density is a tensor. Many thanks in advance. Gustav (talk) 15:21, 25 April 2021 (UTC)
- Agree with Gleedadswell, 144.122.162.45, 64.179.179.8. A 'flux' is the surface integral of a 'flux density', so it is the dot product with the surface normal. If the 'flux density' is a vector, such as magnetic field, electric field, current density, Poynting vector, fluid velocity, etc., the flux is a scalar. If the flux density is a 2nd rank tensor, the flux is a vector. --ChetvornoTALK 16:57, 25 April 2021 (UTC)
- @Gleedadswell: I agree with you. This page is totally confusing. I think the problem concern more articles and this lead a lot of misunderstandings. I have these 3 definitions that should be checked, which if correct, would solve the problems a bit and would be a start:
- Flux or Rate: Quantity of objects that cross a surface in a unit of time
- Fluence: Quantity of objects that cross a unit of surface
- Flux density or Fluence Rate: Quantity of objects that cross a unit of surface in a unit of time Agador88 (talk) 11:07, 30 May 2021 (UTC)
- Flux density refers to the rate of change in some quantity with respect to area, flux refers to the total change in some quantity over a given area found either by multiplying the area by the flux density, or by integrating the flux density with respect to area. Flux density is to flux as velocity is to distance. — Preceding unsigned comment added by 125.236.222.58 (talk) 03:23, 13 June 2022 (UTC)
- I agree with this paragraph except for the last sentence. Flux density is integrated wrt area to give you flux. Velocity is integrated wrt TIME to give you distance. So that is a misleading comparison, since we are talking about density (i.e. over area). Steveraysteveray (talk) 15:07, 3 August 2022 (UTC)
- Totally agree. Flux and flux density are confusing terms in many text book and college education now. Flux should be consistently defined as the "flow rate", which is some quantity per second and the flux density is the flow rate per unit area, which depends on the property of the surface such as its orientation. 35.3.154.15 (talk) 18:39, 19 January 2023 (UTC)
Even without the complication of tensors, I am seeing three distinct concepts here. If v is a vector field and dA is the normal vector to an infinitesimal area then the three are:
- v, a vector field
- v · dA, a scalar field (at least on the surface), and
- ∫ v·dA, a scalar.
If we can get consensus on what to name all three of these, I volunteer to make edits to the article. —Quantling (talk | contribs) 21:27, 19 January 2023 (UTC)
- @Agador88 and 35.3.154.15: Just want to point out that neither flux nor flux density necessarily are a "rate" or have anything to do with time. In transport phenomena they are, but not in electromagnetic field theory, for example. --ChetvornoTALK 18:10, 20 January 2023 (UTC)
- 1) is the vector field that
- 2) is the flux density of (which will vary smoothly for nearby surfaces with nearby boundary)
- 3) is the flux of the vector field thru the surface, so long as the surface is defined.
- The important issue is to distinguish an open surface Area (with a boundary line)
- ... for water flow or magnetic field change (Faraday's Law),
- from a closed surface Area (separating inside from outside) ... for sound intensity or Gauss' Law
- ANY ONE who intends to integrate a rank-2 tensor thru a surface will expect the rank to decrease by 1
- - do not confuse newbies by claiming that flux is a vector.
- by this, I mean either *guide* the reader thru Maxwell's plainspoken quote, or get rid of it
- (pretty sure he knew that "flux is the integral of flux" is a bad definition).
- Your own "Flux as a vector field" is actually not
- ... it is a (hard-to-follow) flux OF a vector field thru an undefined Area 2601:541:680:98A0:5D07:1519:F42B:1DB1 (talk) 23:10, 24 November 2024 (UTC)
Wiki Education assignment: Plant Behavior 2022
[edit]![]() This article was the subject of a Wiki Education Foundation-supported course assignment, between 28 March 2022 and 17 June 2022. Further details are available on the course page. Student editor(s): Kay Kang 1 (article contribs).
This article was the subject of a Wiki Education Foundation-supported course assignment, between 28 March 2022 and 17 June 2022. Further details are available on the course page. Student editor(s): Kay Kang 1 (article contribs).
— Assignment last updated by Gonet99 (talk) 19:16, 13 June 2022 (UTC)
- @Noosa.N: You might like to confirm what article is intended as Flux is a physics topic. Johnuniq (talk) 04:34, 1 June 2022 (UTC)
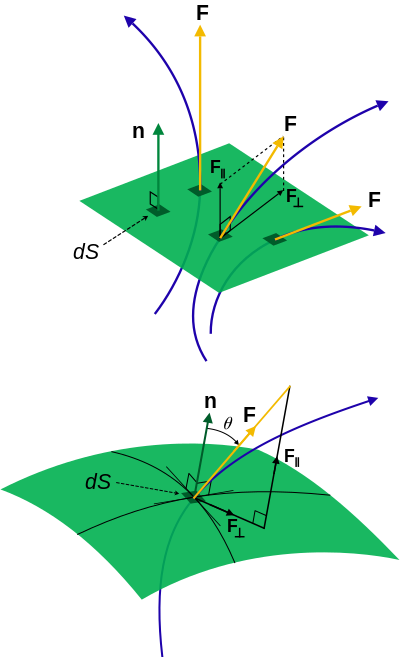
Should be only perpendicular component, not “parallel”
[edit]See description of second image Morganciliv (talk) 21:12, 26 January 2024 (UTC)
- I think this refers to the caption "
Only the parallel component contributes to flux because it is the maximum extent of the field passing through the surface at a point, the perpendicular component does not contribute.
" The idea seems to have been added on 20 July 2016. It looks correct although possibly confusing because the diagram shows that "parallel" means parallel to the normal to the surface. That means the flux is perpendicular to the surface. Johnuniq (talk) 01:36, 27 January 2024 (UTC)- Yes, the subscript ⊥ always means perpendicular to the surface, which equals v·n
- I will try to fix the diagram this (also to show how the parallel component does not go thru that surface) 2601:541:680:98A0:5D07:1519:F42B:1DB1 (talk) 23:19, 24 November 2024 (UTC)
- Is v⊥ a scalar or vector? If the latter, it would be , yes? —Quantling (talk | contribs) 19:36, 25 November 2024 (UTC)












